https://www.acmicpc.net/problem/1865
1865번: 웜홀
첫 번째 줄에는 테스트케이스의 개수 TC(1 ≤ TC ≤ 5)가 주어진다. 그리고 두 번째 줄부터 TC개의 테스트케이스가 차례로 주어지는데 각 테스트케이스의 첫 번째 줄에는 지점의 수 N(1 ≤ N ≤ 500),
www.acmicpc.net
벨만포드(Bellman ford) 알고리즘을 사용해야하는 문제입니다.
우선 문제부터 간단하게 요약하면,
도로는 양의 간선으로 양방향으로 구성되고, 웜홀은 음의 간선으로 단방향으로 구성됩니다. 이렇게 그래프가 구성되었을 때, random한 출발지 A 에서 다시 A로 간선들을 타고 되돌아 왔을 때, 음의 weight를 가지는 것이 하나라도 존재하면, YES를 아니면 NO를 출력해야 합니다.
실제로 문제를 읽어보는 것을 추천합니다.
아이디어와 실제 구현을 설명해 보도록 하겠습니다.
<Solution>
우선 가장 중요한 아이디어는 "출발지 A 에서 다시 출발지 A로 되돌아 와야 한다" 라는 것입니다.
그래프에서 이렇게 되돌아 오게 되면,
| 1. 이러한 경로는 cycle을 구성합니다. 2. 이 cycle 안에 속해있는 간선들을 더하면 음의 weight을 가져야 합니다. 3. 이 이야기는 Bellman ford 알고리즘의 "음수 순환"을 찾는 문제와 완전히 동일합니다. |
이렇게 문제를 재해석 할 수 있습니다.
이제 여기에서 한가지의 문제점이 발생하게 됩니다. Bellman ford 알고리즘은 특정한 점(start node) 에서 다른 점들로 가는 최단 거리를 구하는 목적인데 출발지가 고정이 아닙니다.
이 문제는 새로운 node 하나를 추가하고, 그 노드로 부터 다른 모든 node들로의 단방향 간선의 weight를 0으로 둠으로 써 해결할 수 있습니다. 이것이 무슨말인지 그림으로 좀더 살펴봅시다.
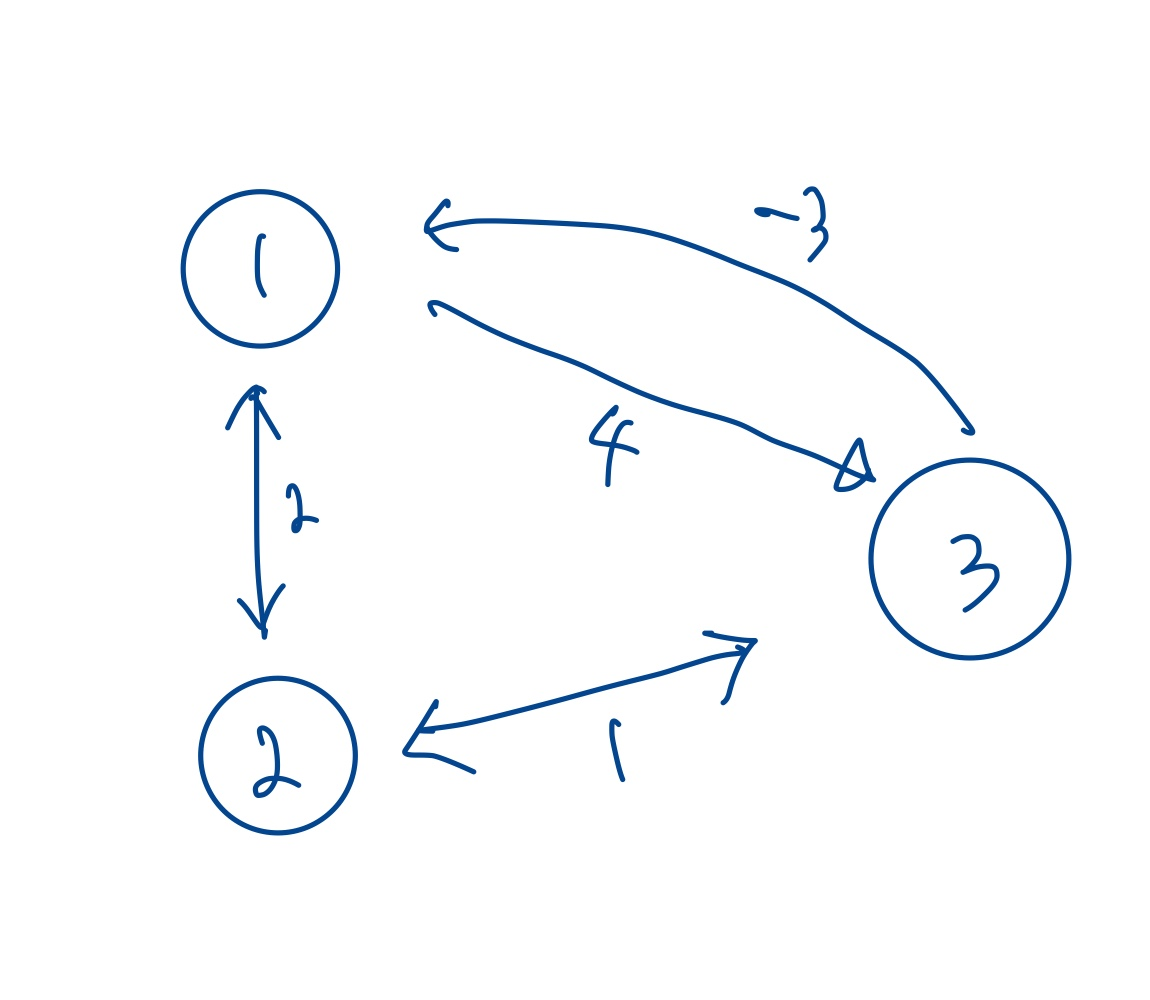
다음과 같은 그래프가 있다고 가정을 해봅시다. 여기에서 3번 node에서 1번 node를 향하는 -3이 웜홀입니다.
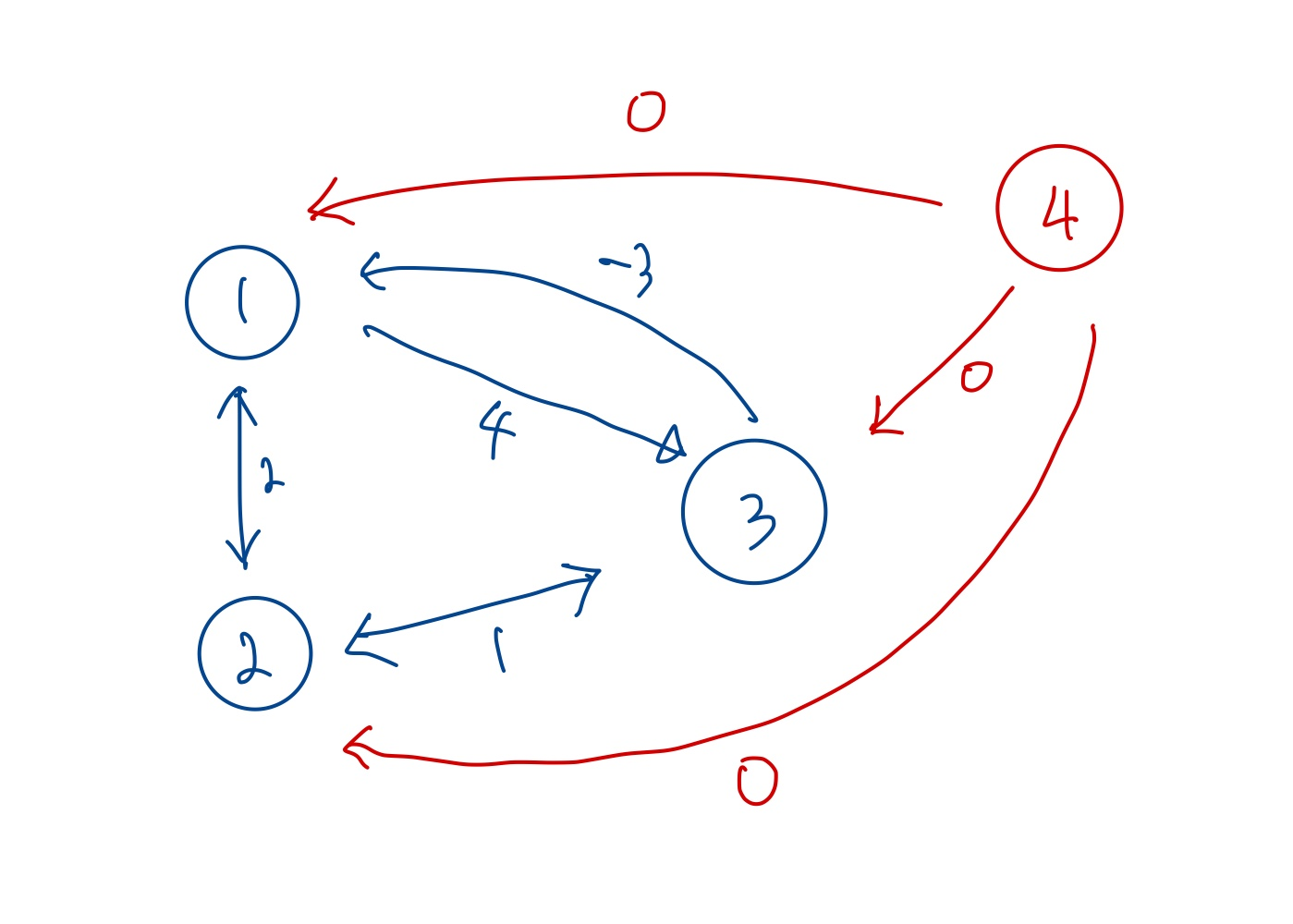
이 때, 다음과 같이 4번 node를 새로 만들어서 1번, 2번, 3번 node로 향하는 단방향 간선의 weight이 0이라고 둡니다. 그리고 출발지를 4번 node로 해서 Bellman-ford 알고리즘을 사용하면, 우리는 각각의 출발지에서 출발을 해서 음의 순환이 존재하는지 검사하는 상황과 똑같은 상황을 한번에 해결 할 수 있습니다.
실제 구현은 아래와 같습니다.
import sys
from collections import defaultdict
# question : 웜홀은 1->2로가는 웜홀이 여러개일수 있는가??? 일단 없다하고 풀어보자
def bellman_ford(graph, start_node):
to_return = [True]
# num node
N = len(graph) - 1
# start node에서 타 노드로의 거리를 담는 array(index = node number)
distance = [int(2e9)]*(N+1)
distance[start_node] = 0
for j in range(N):
for i in range(1,N+1):
for edge in graph[i]:
start = i
end = edge[0]
cost = edge[1]
if distance[start] == int(2e9):
continue
if distance[end] > distance[start] + cost:
if j != N-1:
distance[end] = distance[start] + cost
else:
# 갱신이 되면 음수순환이 존재한다는 것임
# 해당하는 node 들을 minus int(2e9)로 만들기
distance[end] = -int(2e9)
to_return[0] = False
to_return.append(distance)
return to_return
TC = int(sys.stdin.readline().rstrip())
for _ in range(TC):
N, M, W = list(map(int, sys.stdin.readline().rstrip().split()))
# build graph
tmp_graph = [defaultdict(list) for _ in range(N+1)]
graph = [[] for _ in range(N+1+1)] # addition 1 for node n+1 (which is start point)
# get Roads (bidirectional) & should remove multiple roads
for _ in range(M):
S, E, T = list(map(int, sys.stdin.readline().rstrip().split()))
tmp_graph[S][E].append(T)
tmp_graph[E][S].append(T)
# get worm holes
for _ in range(W):
S, E, T = list(map(int, sys.stdin.readline().rstrip().split()))
tmp_graph[S][E].append((-1)*T)
# print(f'graph before remove:\n{tmp_graph}')
# remove
for i in range(1, N+1):
for key in iter(tmp_graph[i]):
graph[i].append((key, min(tmp_graph[i][key])))
# print(f'graph after remove:\n{graph}')
# build start point
for i in range(1,N+1):
graph[N+1].append((i,0))
# print(f'graph include new node:\n{graph}')
tf, path = bellman_ford(graph, N+1)
if tf:
print("NO")
else:
print("YES")'코딩테스트 > Python 문제풀이' 카테고리의 다른 글
| [백준] N과 M (2) (0) | 2022.06.25 |
|---|---|
| [백준] 2048 (Easy) (0) | 2022.06.25 |
| [백준] 최단경로 (0) | 2022.06.24 |
| [백준] 곱셈 (0) | 2022.06.24 |
| [백준] 특정한 최단 경로 (0) | 2022.06.24 |