https://www.acmicpc.net/problem/14500
14500번: 테트로미노
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다. 정사각형은 서로 겹치면 안 된다. 도형은 모두 연결되어 있어야 한다. 정사각형의 변
www.acmicpc.net
dfs방법과, 직접 구현하는 방식 두 방식으로 문제를 해결하였습니다. 총 두가지 풀이에 대해 설명해 보겠습니다.
우선 문제부터 간단하게 요약하면,
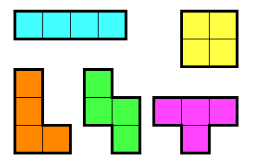
이렇게 4개의 정사각형으로 만들어진 조각들로 숫자들이 놓인 N x M 크기의 종이안의 합이 최대가 되는 경우의 값을 구하는 문제입니다. 실제로 문제를 읽어보는 것을 추천합니다.
<Solution>
총 두가지의 방법으로 해결하였는데 각각의 방법에 대해 설명해 보겠습니다.
방법1. 직접 구현을 통한 해결
간단하게 하나의 예시를 통해 설명해 보겠습니다.
우선 우리는 block들을 1*4, 2*2, 2*3, 3*2, 4*1의 집합으로 분해할 수 있습니다. 이것이 무슨 이야기인가 하면,
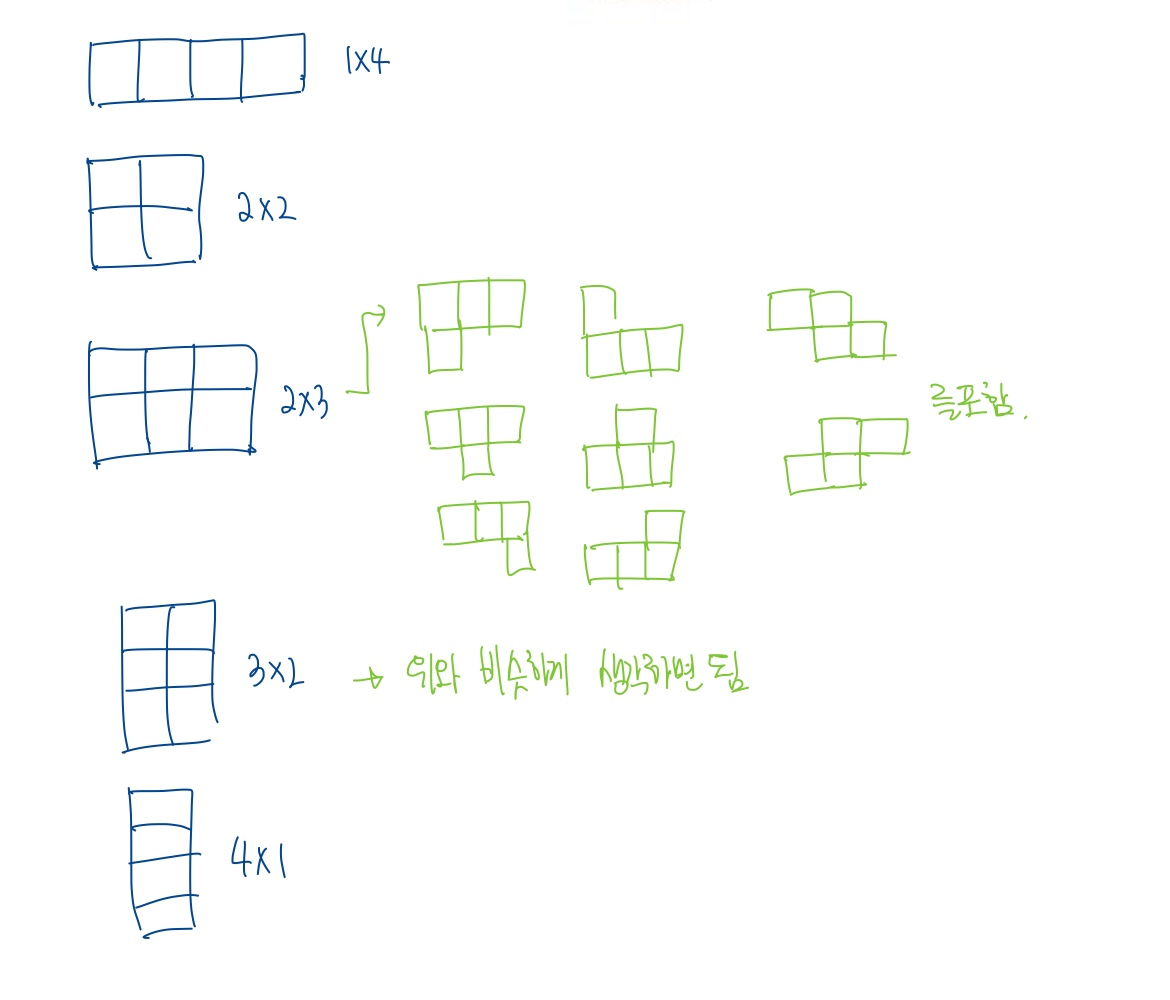
위와 같이 블록들을 분류할 수 있습니다.
그러면, 간단하게 2x3의 블록들에 대해 조사를 한다고 가정하면,
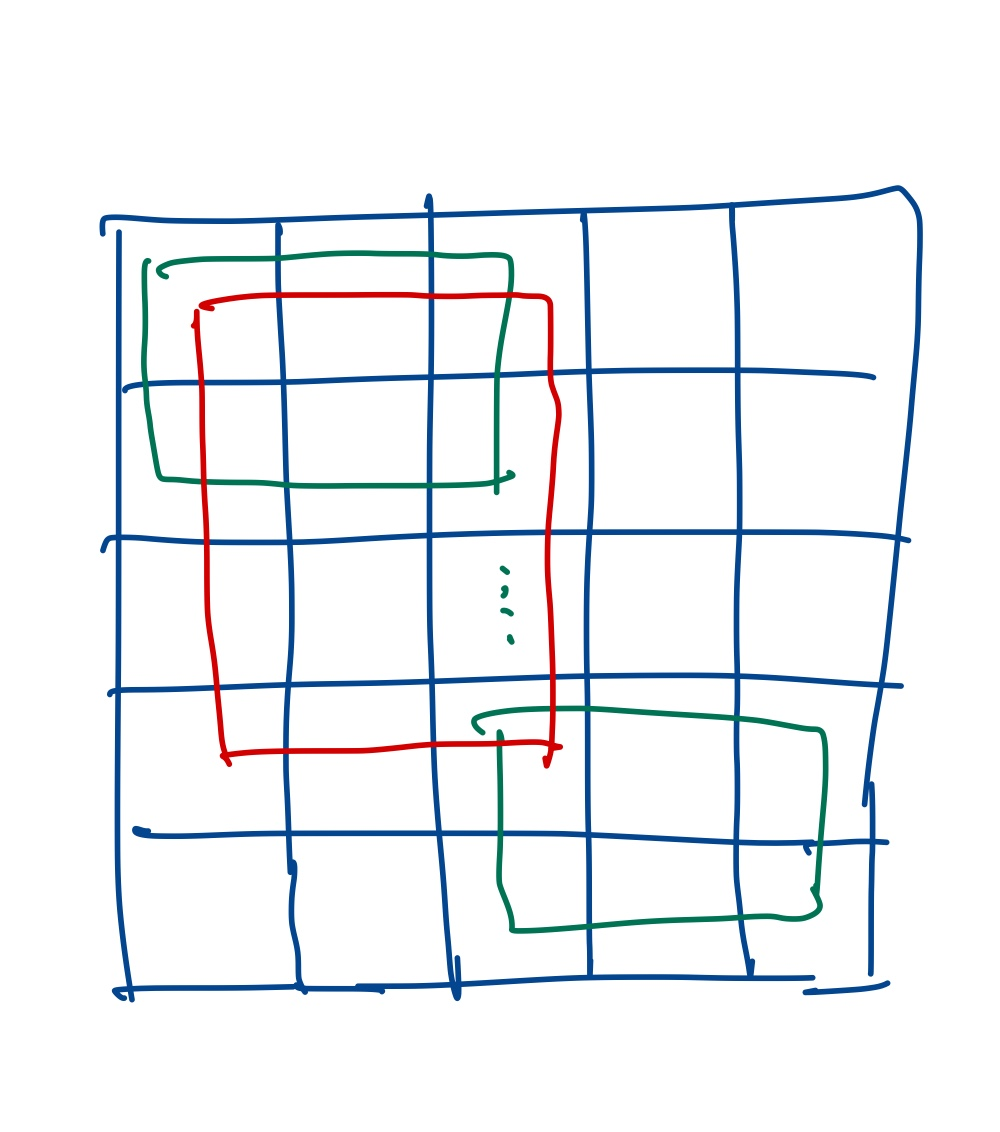
위의 초록색 칸들을 조사하는 것과 같은데, 이것은 출발지가 빨간색 박스안에 있는 것을 조사하는 것으로 생각할 수 있습니다.
이렇게 각각의 초록색 박스에 대해 2*3안의 테트로미노에 대해 조사하면 됩니다. 위의 경우에는
row 0~3
column 0~2에 대해 조사하면 됩니다.
이처럼 각각의 size에 대해 전부 계산을 하면 됩니다. 사실 저의 실제 구현에서는
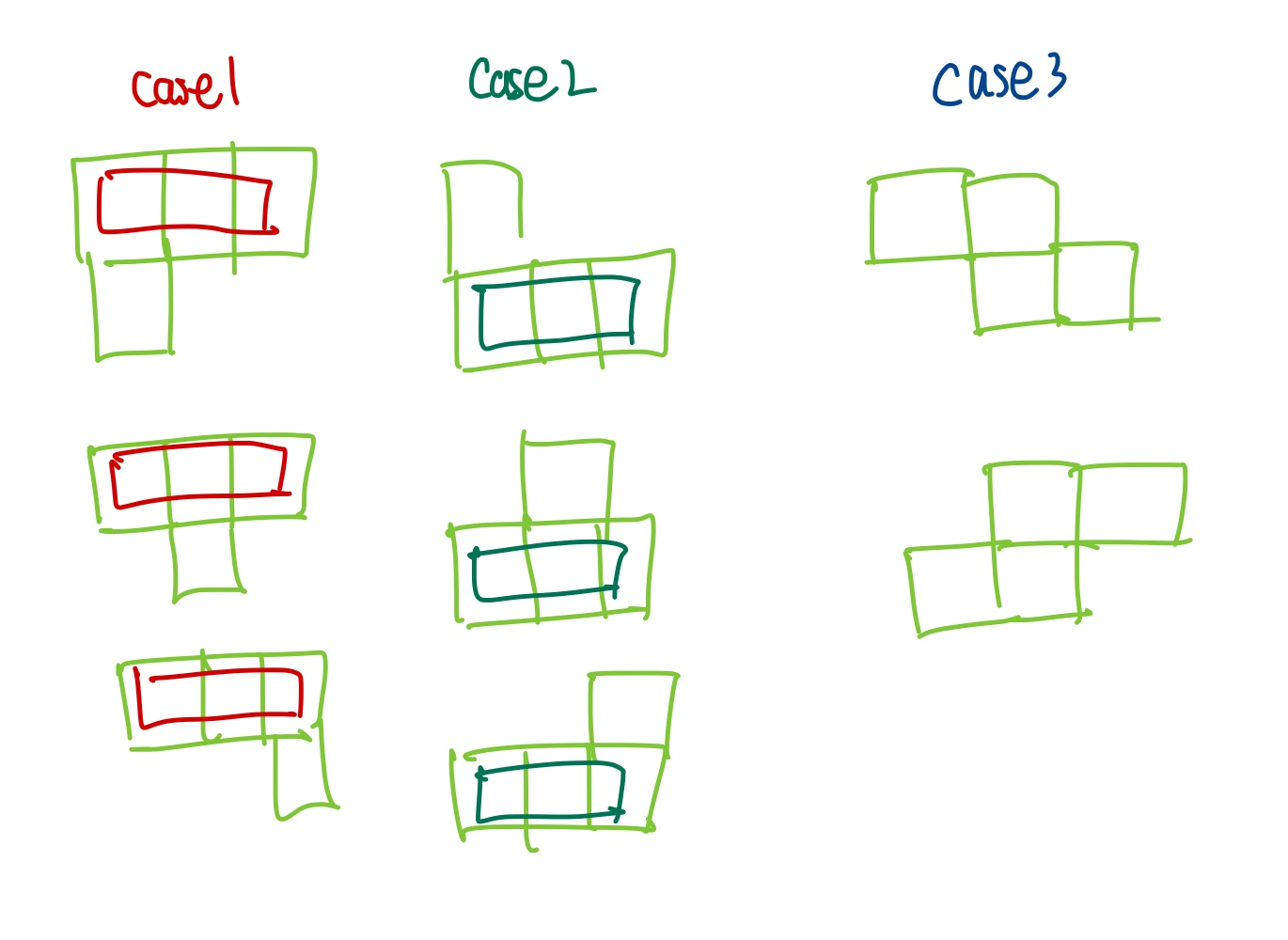
다음과 같이 묶어서 계산을 해서 중복된 계산을 최대한 피해주었는데, 누적합과 같은 것을 이용하면 좀더 속도를 올릴 수 있을 것이라 생각합니다.
실제 구현은 아래와 같습니다. 백준 기준으로 pypy가 아닌 python에서도 돌아가는 것을 확인할 수 있습니다. (dfs의 경우 일부 가지치기를 하지 않으면, pypy에서만 돌아감)
import sys
N, M = list(map(int, sys.stdin.readline().rstrip().split()))
graph = [list(map(int, sys.stdin.readline().rstrip().split())) for _ in range(N)]
# find_available
def available_blocks(N, M):
ret = []
blocks = [(1,4),(2,3),(2,2),(3,2),(4,1)]
for block in blocks:
r,c = block
if r<= N and c<= M:
ret.append(block)
return ret
available = available_blocks(N, M)
# print(f'available : {available}')
max_val = -1
M+=1
N+=1
for e in available:
# print(f'current e : {e}')
if e == (1,4):
for i in range(M-4): # c
for j in range(N-1): # r
# prefix sum might be better way but for now just sum all one by one
sum = graph[j][i] + graph[j][i+1] + graph[j][i+2] + graph[j][i+3]
max_val = max(sum, max_val)
# print("1,4")
# print(max_val)
if e == (4,1):
for i in range(M-1): # c
for j in range(N-4): # r
# prefix sum might be better way but for now just sum all one by one
sum = graph[j][i] + graph[j+1][i] + graph[j+2][i] + graph[j+3][i]
max_val = max(sum, max_val)
# print("4,1")
# print(max_val)
if e == (2,3):
for i in range(M-3):
for j in range(N-2):
tmp1 = graph[j][i] + graph[j][i+1] + graph[j][i+2] + (max(graph[j+1][i], graph[j+1][i+1], graph[j+1][i+2]))
tmp2 = graph[j+1][i] + graph[j+1][i+1] + graph[j+1][i+2] + (max(graph[j][i], graph[j][i+1], graph[j][i+2]))
tmp3 = graph[j+1][i] + graph[j][i+1] + graph[j+1][i+1] + graph[j][i+2]
tmp4 = graph[j][i] + graph[j][i+1] + graph[j+1][i+1] + graph[j+1][i+2]
max_val = max(max_val, tmp1, tmp2, tmp3, tmp4)
# print("2,3")
# print(max_val)
if e == (3,2):
# just transpse graph
graph = list(zip(*graph))
for i in range(N-3):
for j in range(M-2):
tmp1 = graph[j][i] + graph[j][i+1] + graph[j][i+2] + (max(graph[j+1][i], graph[j+1][i+1], graph[j+1][i+2]))
tmp2 = graph[j+1][i] + graph[j+1][i+1] + graph[j+1][i+2] + (max(graph[j][i], graph[j][i+1], graph[j][i+2]))
tmp3 = graph[j+1][i] + graph[j][i+1] + graph[j+1][i+1] + graph[j][i+2]
tmp4 = graph[j][i] + graph[j][i+1] + graph[j+1][i+1] + graph[j+1][i+2]
max_val = max(max_val, tmp1, tmp2, tmp3, tmp4)
graph = list(zip(*graph))
# print("3,2")
# print(max_val)
if e == (2,2):
for i in range(M-2):
for j in range(N-2):
sum = graph[j][i] + graph[j+1][i] + graph[j][i+1] + graph[j+1][i+1]
max_val = max(max_val, sum)
# print("2,2")
# print(max_val)
print(max_val)
방법 2.DFS 방식을 이용한 구현
이 문제를 위의 방식으로 해결하고, 시간이 생각보다 많이 나와서, 인터넷을 찾아보다 발견한 방법과, 다른 분의 풀이를 조금 참고하여 나은 solution을 만든 것입니다.
우선 ㅗ ㅏ ㅓ ㅜ 의 모양을 제외한 모든 모양들은 DFS를 깊이 4로 하는 동안 생기는 모양들인 것을 알 수 있습니다.
따라서 DFS를 깊이 4까지 하면 "ㅗ ㅏ ㅓ ㅜ" 모양을 제외한 모든 모양들에 대한 search가 진행 되는 것을 알 수 있습니다.
따라서 중간에 DFS의 깊이가 2인 경우 ㅗ ㅏ ㅓ ㅜ 모양에 대해 직접 계산을 하는 방식으로 구현을 하였습니다.
위에서 설명한 방식인 일반적인 DFS로는 pypy가 아닌 환경에서는 통과가 안되는데 가지치기를 할 방법이 있습니다.
만약 블록을 2개 더했다고 생각해봅시다.
그리고 이때 sum 값을 10이라고 생각해봅시다. 만약 paper에 놓인 가장 큰 값이 7이라고 가정하면, 현재부터 DFS를 해서 나올수 있는 값이 아무리 잘나와 봤자 10+7+7인 24인 것을 알 수 있습니다. 하지만 만약 이전의 결과중 24보다 큰 결과가 있다면, 이 경우 DFS를 더이상 진행해 줄 필요가 없습니다.
따라서 다음과 같이 가지치기를 할 수 있음을 알 수 있습니다.
# branching
if (4-cnt) * max_e + sum_ <= max_val:
return
실제 구현은 아래와 같습니다.
import sys
import itertools
N, M = list(map(int, sys.stdin.readline().rstrip().split()))
graph = [list(map(int, sys.stdin.readline().rstrip().split())) for _ in range(N)]
visited = [[False]* M for _ in range(N)]
max_val = -1
dir_r = [0,0,-1,1] # right left up down
dir_c = [1,-1,0,0]
sum_ = 0
def dfs(r, c, cnt): # 0,0,0
global max_e
global sum_
global max_val
if visited[r][c]:
return
# branching
if (4-cnt) * max_e + sum_ <= max_val:
return
visited[r][c] = True
sum_ += graph[r][c]
cnt += 1
if cnt == 4:
max_val = max(max_val, sum_)
sum_-=graph[r][c]
visited[r][c] = False
return
if cnt == 2:
# find non searched index
non_searched = []
for i in range(4):
r_ = r+ dir_r[i]
c_ = c+ dir_c[i]
if 0<= r_ < N and 0<= c_ < M and not visited[r_][c_]:
non_searched.append((r_,c_))
if len(non_searched) >= 2:
nPr = itertools.combinations(non_searched,2)
for e in nPr:
max_val = max(max_val, sum_ + graph[e[0][0]][e[0][1]] + graph[e[1][0]][e[1][1]])
for i in range(4):
new_r = r + dir_r[i]
new_c = c + dir_c[i]
if 0<= new_r < N and 0<= new_c < M and not visited[new_r][new_c]:
dfs(new_r, new_c, cnt)
sum_-=graph[r][c]
visited[r][c] = False
# find max
max_e = max(map(max,graph))
for i in range(N):
for j in range(M):
dfs(i,j,0)
print(max_val)'코딩테스트 > Python 문제풀이' 카테고리의 다른 글
| [백준] 연구소 (0) | 2022.07.22 |
|---|---|
| [백준] 퇴사 (0) | 2022.07.22 |
| [백준] 주사위 굴리기 (0) | 2022.07.21 |
| [백준] 연산자 끼워넣기 (0) | 2022.07.21 |
| [백준] 상어 초등학교 (0) | 2022.07.21 |